https://www.acmicpc.net/problem/1332
브루트포스 문제
시간복잡도
O(2^N), N = 50, 2^50 = 1,125,899,906,842,624에 가깝다.
때문에, 문제 분류는 브루트포스만 적혀있음에도
재귀/그래프 탐색/dp 뭐든간에 같이 쓰고 prune, memo 등으로 최적화 해야 한다.
나름 최단경로 문제이므로, 나는 BFS를 썼다.
최적화로 다음 경우를 쳐낼 수 있으면 풀릴 것 같다.
50 10
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
+ 개인적으로는 안좋은 문제같다.
복잡도 측면에서, 이정도 최적화로 통과하겠다는 확신을 가지기 어렵고,
최적화 -> 제출 -> 틀렸습니다를 n번 반복해야 하는 문제로 인식했다.
고수들도 이왜맞 의견이었고, 정답률도 21%다.
-----------------------------------------------------------------
문제 자체는 i+1, i+2를 선택할 수 있으므로, 피보나치 수열 꼴이 된다.
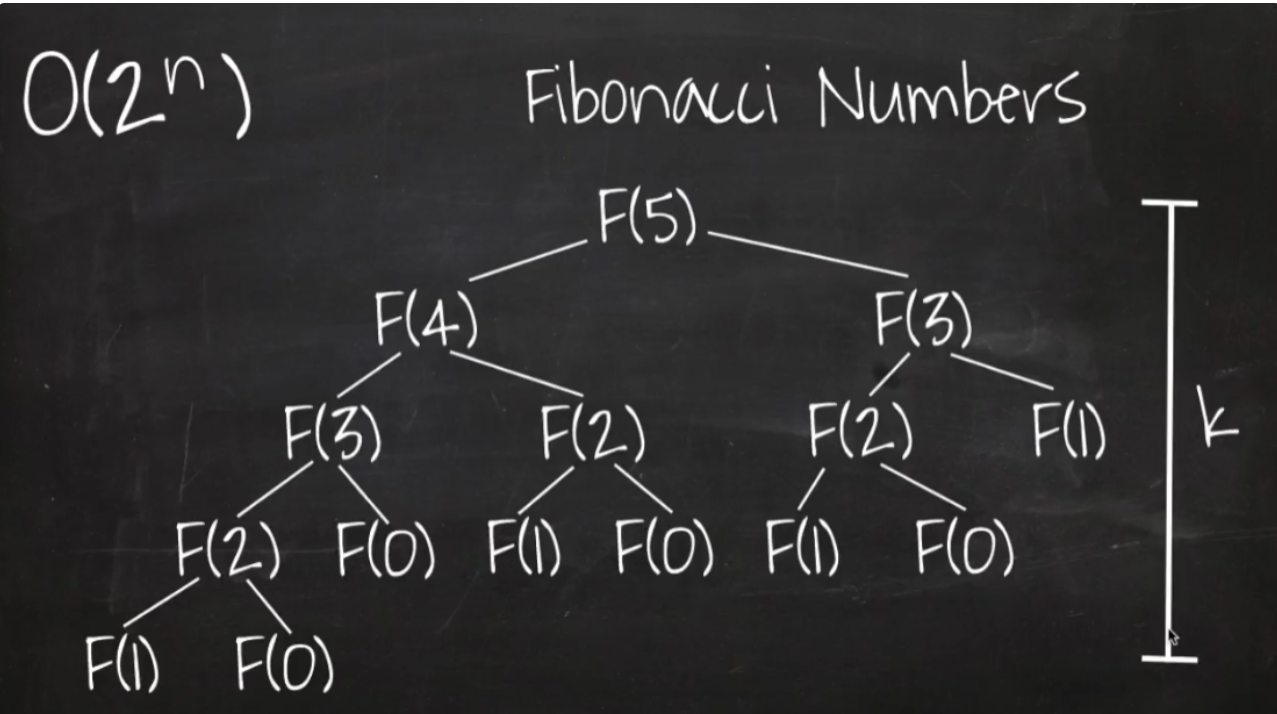
그래서 재귀 + 중복 탐색을 dp로 memo하면 될 것 같지만, 중복 탐색을 어떻게 정의할 것인가가 어렵다.
1. 푼 문제수(depth)가 같아도 max와 min이 달라진다. 이를 모두 기록해야해서, 중복 탐색의 범주가 줄어든다.
2. diff = max - min만 기록하면 안된다. diff와 상관없이, 다음 탐색에 min이 작은게 유리할 수도, max가 큰게 유리할 수도 있다.
끽해야 min이 같고 max가 더 크면 채택 / max가 같고 min이 더 작으면 채택 등이 가능할 것 같다.
결국, 유의미하게 기록할 수 있는게 모호해서 브루트포스와 같아진다.
그래서,
BFS로 max - min >= V인 지점을 찾으면 종료시키는 코드로 1%에서 메모리초과를 받았고,
vst를 Set으로 놓고 key를 i:min:max 문자열로 했더니 허무하게 통과됐다.
cnt는 어차피 BFS로 달성만 하면 최단경로이므로 vst에 key로 기록할 필요가 없다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.HashSet;
import java.util.Queue;
import java.util.Set;
import java.util.StringTokenizer;
public class Main {
static class State {
int i, min, max, cnt;
State(int i, int min, int max, int cnt) {
this.i = i;
this.min = min;
this.max = max;
this.cnt = cnt;
}
// 문자열로 상태 구분: "index:min:max"
String key() {
return i + ":" + min + ":" + max;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
int[] P = new int[N];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
P[i] = Integer.parseInt(st.nextToken());
}
Queue<State> q = new ArrayDeque<>();
Set<String> visited = new HashSet<>();
// 조건에서, 1번 문제는 반드시 풀어야 한다.
State start = new State(0, P[0], P[0], 1);
q.offer(start);
visited.add(start.key());
while (!q.isEmpty()) {
State s = q.poll();
if (s.max - s.min >= V) {
System.out.println(s.cnt);
return;
}
if (s.i + 1 < N) {
int ni = s.i + 1;
int nmin = Math.min(s.min, P[ni]);
int nmax = Math.max(s.max, P[ni]);
State next = new State(ni, nmin, nmax, s.cnt + 1);
if (visited.add(next.key())) {
q.offer(next);
}
}
if (s.i + 2 < N) {
int ni = s.i + 2;
int nmin = Math.min(s.min, P[ni]);
int nmax = Math.max(s.max, P[ni]);
State next = new State(ni, nmin, nmax, s.cnt + 1);
if (visited.add(next.key())) {
q.offer(next);
}
}
}
System.out.println(N);
}
}'[백준] PS > Java' 카테고리의 다른 글
| [백준 1715] 카드 정렬하기 - JAVA (0) | 2025.05.10 |
|---|---|
| [백준 2064] IP 주소 - JAVA (0) | 2025.05.09 |
| [백준 1327] 소트 게임 - JAVA (0) | 2025.05.06 |
| [백준 1599] 민식어 - JAVA (0) | 2025.03.04 |
| [백준 1647] 도시 분할 계획 - JAVA (0) | 2025.03.04 |