위상 정렬 (Topological Sorting)
유향 비순환 그래프(DAG)의 정점을 변의 방향을 거스르지 않도록 나열하는 정렬 기법이다.
탐색 기법도 맞지만 정렬 기법이라는 표현이 본질에 더 가깝다.
이벤트/작업 스케쥴링, 의존성 관리 등 순서를 정해야 할 때 사용할 수 있다.
정의만 들어서는 잘 이해가 가지않는다.
보통 예시로 선수 과목(혹은 커리큘럼/이수 체계도)를 든다.

세 과목을 모두 듣기 위해서는 자료구조 -> 알고리즘 -> 고급 알고리즘 순서로 과목을 들어야한다.
각 과목을 그래프의 정점(혹은 노드)로 치환했을 때,
자료구조 -> 알고리즘 -> 고급 알고리즘 이라는 이수 순서를 구하는 것이 위상 정렬이다.
위상 정렬의 종류
진입 차수(Indegree) 기반, DFS/BFS 기반, DFS를 변형하여 사전식으로 정렬된 결과를 도출하는 Lexicographical 방법 등이 있다.
여러 기반과 변형 방법은 제쳐두고, 위상 정렬을 수행하는 방법이 한 가지가 아님을 기억하면 된다.
오늘은 Indegree기반의 Kahn's 알고리즘을 다룬다. (사실상 동작이 BFS 기반과 흡사하여, Indegree+BFS라고 봐도 된다.)
Kahn's 알고리즘의 특징
1. 진입 차수(Indegree) 기반의 방식이다.
진입 차수가 0인 정점들을 큐에 넣고, 인접한 정점들의 차수를 낮추는 방식을 반복한다.
2. 정렬 순서가 달라질 수 있다.
A를 위해 B와 C가 필요하다면, B->C->A, C->B->A 둘다 가능하다.
사전순으로 표현해야 한다면 Lexicographical 위상 정렬을 사용한다.
3. 각 정점은 한번만 탐색한다.
그래프 구현체가 인접 리스트 일 때 O(V+E), 인접 배열일 때 O(V^2)인 이유이다.
또한 어차피 한번만 탐색하므로, 방문 체크(visited 같은) 배열이 필요 없다.
4. 사이클이 있음을 찾아낼 수 있다.
정렬이라는 목적과 어긋나지만, 모든 정점에 도달하기 전에 큐가 비어있다면
위상 정렬이 실패했음과 동시에 사이클이 존재함을 알 수 있다.
Kahn's 알고리즘의 적용 조건
1. 사이클이 없어야 한다.
사이클이 있다면, "각 정점은 한번만 탐색한다."라는 3번 특징에 어긋난다.
2. 유향 그래프여야 한다.
비유향 그래프 혹은 양방향 그래프라면(둘은 다르다), 이는 사이클이 있음을 의미한다. 1번 조건에 어긋난다.
1,2번을 모두 만족하는 그래프를
DAG (Direct Acyclic Graph): 순환하지 않는 방향 그래프
라고 칭한다. 즉, Kahn's 알고리즘을 적용하려면 DAG여야 한다.
Kahn's 알고리즘의 동작 순서
기본적으로, 큐로 구현한다. 다른 자료구조를 쓸 수도 있다.
1. 진입 차수가 0인 노드 큐에 넣는다.
2. 인접한 노드들의 진입 차수를 1낮춘다.
해당 과정을 반복한다. 진입 차수가 뭘까? 그림으로 알아보자.

진입 차수란, 어떤 노드의 인접 노드에서 진입하는 방향인 간선의 개수를 뜻한다.
(노드4는 인접한 노드3, 노드6 에서 진입하므로 노드4의 진입 차수는 2이다.)
위의 그래프에서는 노드1에 아무것도 진입하지 않았으므로 큐에 넣는다. 여러개 있었다면 모두 넣었을 것이다.
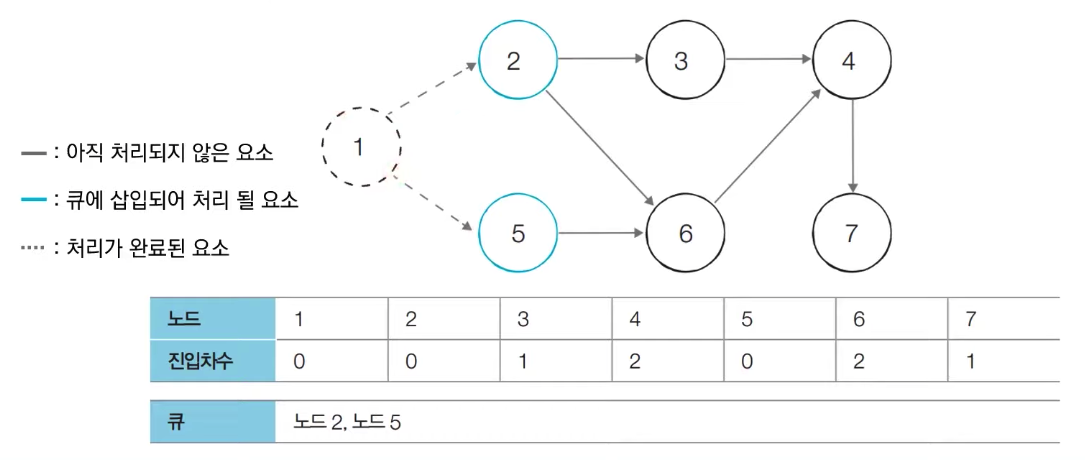
큐에 담긴 노드1를 pop()한다. 인접한 노드(2,5)들의 진입 차수를 1씩 낮춘다.
이때, 노드2와 노드5의 진입 차수가 0이 되었으므로, 큐에 넣는다. (진입 차수가 0이 아니라면 넣지 않는다.)
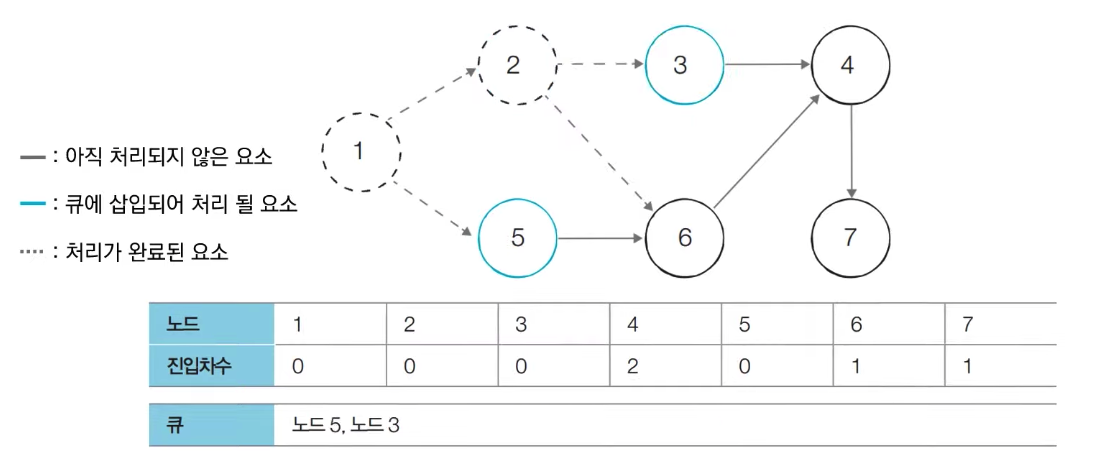
큐에 담긴 노드2를 pop()한다. 인접한 노드(3,6)의 진입 차수를 1씩 낮춘다.
해당 과정을 반복한다.
결국 모든 정점을 한번만 방문하며 진입 차수를 0으로 만들 것이고,
정렬 결과는 큐에서 pop()한 순서 1 → 2 → 5 → 3 → 6 → 4 → 7 가 된다.
유의할 점
매 순간마다 모든 노드를 탐색하며, 진입 차수가 0인 노드를 찾을 필요가 없다. (초기 한번만 탐색한다.)
큐에 있는 노드를 pop()하며 차수를 낮출 때, 인접한 노드가 차수가 0인지만 판별하면 된다.
구현 코드는 https://sh3542.tistory.com/18로 대신한다.
기존 BFS에 방문 여부(visited) 대신 진입 차수(degree)를 비교하고, 위상 정렬 결과를 담을 컨테이너를 추가하면 된다.